STDP学习

本教程作者： fangwei123456

生物可解释性的学习规则一直备受SNN研究者的关注。在SpikingJelly中提供了STDP(Spike Timing Dependent Plasticity) 学习器，可以用于卷积或全连接层的权重学习。

STDP(Spike Timing Dependent Plasticity)

STDP(Spike Timing Dependent Plasticity)最早是由 [1] 提出，是在生物实验中发现的一种突触可塑性机制。实验发现，突触权重 受到突触连接的前神经元(pre)和后神经元(post)的脉冲发放的影响，具体而言是：

如果pre神经元先发放脉冲，post神经元后发放脉冲，则突触的权重会增大； 如果pre神经元后发放脉冲，post神经元先发放脉冲，则突触的权重会减小。

生理实验数据拟合的曲线如下图 [2] 所示：

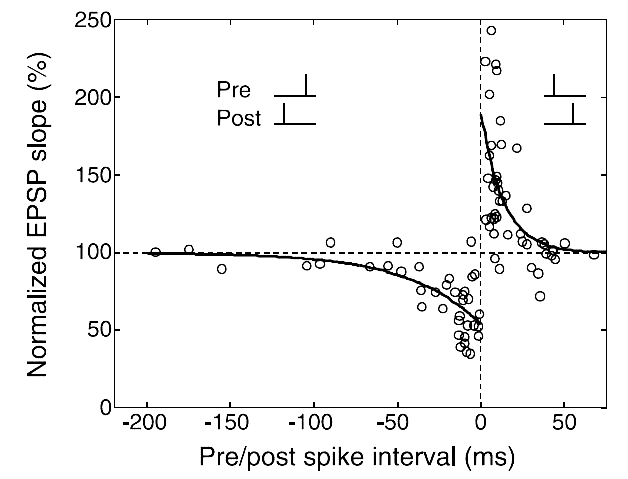
STDP可以使用如下公式进行拟合：

\[\begin{split}\begin{align} \begin{split} \Delta w_{ij} = \begin{cases} A\exp(\frac{-|t_{i}-t_{j}|}{\tau_{+}}) , t_{i} \leq t_{j}, A > 0\\ B\exp(\frac{-|t_{i}-t_{j}|}{\tau_{-}}) , t_{i} > t_{j}, B < 0 \end{cases} \end{split} \end{align}\end{split}\]

其中 \(A, B\) 是突触权重变化的最大值，\(\tau_{+}, \tau_{-}\) 是时间常数。

上述标准的STDP公式在实践中使用较为繁琐，因其需要记录前后神经元所有的脉冲发放时刻。实践中通常使用迹 [3] 的方式来实现STDP。

对于pre神经元 \(i\) 和post神经元 \(j\)，分别使用迹 \(tr_{pre}[i]\) 和 \(tr_{post}[j]\) 来记录其脉冲发放。迹的更新类似于LIF神经元：

\[ \begin{align}\begin{aligned}tr_{pre}[i][t] = tr_{pre}[i][t] -\frac{tr_{pre}[i][t-1]}{\tau_{pre}} + s[i][t]\\tr_{post}[j][t] = tr_{post}[j][t] -\frac{tr_{post}[j][t-1]}{\tau_{post}} + s[j][t]\end{aligned}\end{align} \]

其中 \(\tau_{pre}, \tau_{post}\) 是pre和post迹的时间常数，\(s[i][t], s[j][t]\) 是在 \(t\) 时刻pre神经元 \(i\) 和post神经元 \(j\) 发放的脉冲，取值仅为0或1。

突触权重的更新按照：

\[\Delta W[i][j][t] = F_{post}(w[i][j][t]) \cdot tr_{pre}[i][t] \cdot s[j][t] - F_{pre}(w[i][j][t]) \cdot tr_{post}[j][t] \cdot s[i][t]\]

其中 \(F_{pre}, F_{post}\) 是控制突触改变量的函数。

STDP优化器

spikingjelly.activation_based.learning.STDPLearner 提供了STDP优化器的实现，支持卷积和全连接层，请读者先阅读其API文档以获取使用方法。

我们使用 STDPLearner 搭建一个最简单的 1x1 网络，pre和post都只有一个神经元，并且将权重设置为 0.4：

import torch
import torch.nn as nn
from spikingjelly.activation_based import neuron, layer, learning
from matplotlib import pyplot as plt
torch.manual_seed(0)

def f_weight(x):
    return torch.clamp(x, -1, 1.)

tau_pre = 2.
tau_post = 2.
T = 128
N = 1
lr = 0.01
net = nn.Sequential(
    layer.Linear(1, 1, bias=False),
    neuron.IFNode()
)
nn.init.constant_(net[0].weight.data, 0.4)

STDPLearner 可以将负的权重的更新量 - delta_w * scale 叠加到参数的梯度上，因而与深度学习完全兼容。

我们可以将其和优化器、学习率调节器等深度学习中的模块一起使用。这里我们使用最简单的权重更新策略：

\[W = W - lr \cdot \nabla W\]

其中 \(\nabla W\) 是使用STDP得到的权重更新量取负后的 - delta_w * scale。因而借助优化器可以实现 weight.data = weight.data - lr * weight.grad = weight.data + lr * delta_w * scale。

这可以使用最朴素的 torch.optim.SGD 实现，只需要设置 momentum=0.：

optimizer = torch.optim.SGD(net.parameters(), lr=lr, momentum=0.)

接下来生成输入脉冲，设置 STDPLearner：

in_spike = (torch.rand([T, N, 1]) > 0.7).float()
stdp_learner = learning.STDPLearner(step_mode='s', synapse=net[0], sn=net[1], tau_pre=tau_pre, tau_post=tau_post,
                                    f_pre=f_weight, f_post=f_weight)

接下来送入数据计算。需要注意的是，为了便于画图，我们会将输出数据进行 squeeze()，这样使得 shape = [T, N, 1] 的数据变为 shape = [T]：

out_spike = []
trace_pre = []
trace_post = []
weight = []
with torch.no_grad():
    for t in range(T):
        optimizer.zero_grad()
        out_spike.append(net(in_spike[t]).squeeze())
        stdp_learner.step(on_grad=True)  # 将STDP学习得到的参数更新量叠加到参数的梯度上
        optimizer.step()
        weight.append(net[0].weight.data.clone().squeeze())
        trace_pre.append(stdp_learner.trace_pre.squeeze())
        trace_post.append(stdp_learner.trace_post.squeeze())

in_spike = in_spike.squeeze()
out_spike = torch.stack(out_spike)
trace_pre = torch.stack(trace_pre)
trace_post = torch.stack(trace_post)
weight = torch.stack(weight)

完整的代码位于 spikingjelly/activation_based/examples/stdp_trace.py。

将 in_spike, out_spike, trace_pre, trace_post, weight 画出，得到下图：

这与 [3] 中的Fig.3是一致的（注意下图中使用 j 表示pre神经元，i 表示后神经元，与我们相反）：

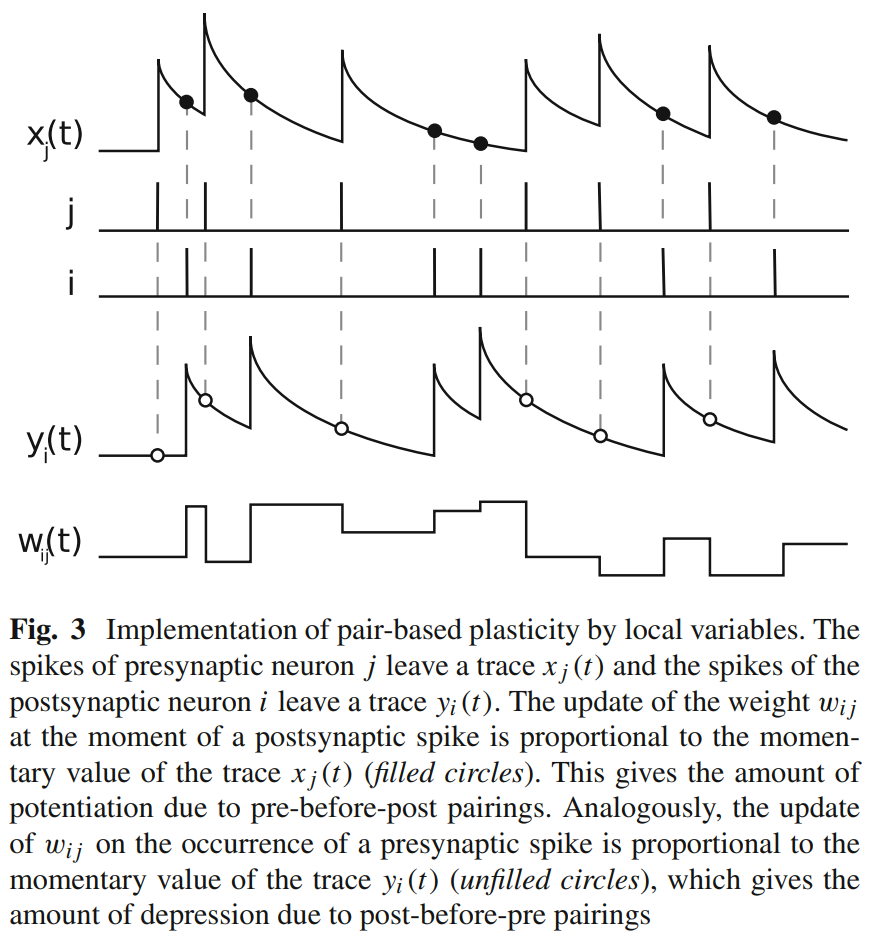
与梯度下降混合使用

在SNN中一种广泛使用STDP的做法是，使用STDP和梯度下降分别训练网路中的不同层。下面介绍如何使用 STDPLearner 实现这一做法。

我们的目标是搭建一个深度卷积SNN，使用STDP训练卷积层，使用梯度下降法训练全连接层。首先定义超参数：

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.optim import SGD, Adam
from spikingjelly.activation_based import learning, layer, neuron, functional

T = 8
N = 2
C = 3
H = 32
W = 32
lr = 0.1
tau_pre = 2.
tau_post = 100.
step_mode = 'm'

我们使用 shape = [T, N, C, H, W] = [8, 2, 3, 32, 32] 的输入。

接下来定义STDP的权重函数以及网络，这里我们搭建的是一个简单的卷积SNN，且使用多步模式：

def f_weight(x):
    return torch.clamp(x, -1, 1.)


net = nn.Sequential(
    layer.Conv2d(3, 16, kernel_size=3, stride=1, padding=1, bias=False),
    neuron.IFNode(),
    layer.MaxPool2d(2, 2),
    layer.Conv2d(16, 16, kernel_size=3, stride=1, padding=1, bias=False),
    neuron.IFNode(),
    layer.MaxPool2d(2, 2),
    layer.Flatten(),
    layer.Linear(16 * 8 * 8, 64, bias=False),
    neuron.IFNode(),
    layer.Linear(64, 10, bias=False),
    neuron.IFNode(),
)

functional.set_step_mode(net, step_mode)

我们希望使用STDP训练 layer.Conv2d，其他层使用梯度下降训练。首先定义使用STDP训练的层类型：

instances_stdp = (layer.Conv2d, )

对于每个类型为 instances_stdp 的层，我们都使用一个STDP学习器：

stdp_learners = []

for i in range(net.__len__()):
    if isinstance(net[i], instances_stdp):
        stdp_learners.append(
            learning.STDPLearner(step_mode=step_mode, synapse=net[i], sn=net[i+1], tau_pre=tau_pre, tau_post=tau_post,
                                f_pre=f_weight, f_post=f_weight)
        )

接下来进行参数分组，将类型为 instances_stdp 的层参数和其他类型的层的参数，分别放置到不同的优化器中。这里我们使用 Adam 作为梯度下降训练的参数的优化器，使用 SGD 作为STDP训练的参数的优化器：

params_stdp = []
for m in net.modules():
    if isinstance(m, instances_stdp):
        for p in m.parameters():
            params_stdp.append(p)

params_stdp_set = set(params_stdp)
params_gradient_descent = []
for p in net.parameters():
    if p not in params_stdp_set:
        params_gradient_descent.append(p)

optimizer_gd = Adam(params_gradient_descent, lr=lr)
optimizer_stdp = SGD(params_stdp, lr=lr, momentum=0.)

在实际任务中，输入和输出应该是从数据集中抽样得到的，我们这里仅仅是做示例，因此手动生成：

x_seq = (torch.rand([T, N, C, H, W]) > 0.5).float()
target = torch.randint(low=0, high=10, size=[N])

接下来就是参数优化的主要步骤了，在实际任务中下面的代码通常会放到训练的主循环中。我们的代码与纯梯度下降会略有不同。

首先清零所有梯度，进行前向传播，计算出损失，反向传播：

optimizer_gd.zero_grad()
optimizer_stdp.zero_grad()
y = net(x_seq).mean(0)
loss = F.cross_entropy(y, target)
loss.backward()

需要注意的是，尽管 optimizer_gd 只会对 params_gradient_descent 中的参数进行梯度下降，但调用 loss.backward() 后整个网络中所有的参数都会计算出梯度，包括那些我们只想使用STDP进行优化的参数。

因此，我们需要将使用梯度下降得到的 params_stdp 的梯度进行清零：

optimizer_stdp.zero_grad()

接下来就是使用STDP学习器计算出参数更新量，然后使用2个优化器，对整个网络的参数进行更新：

for i in range(stdp_learners.__len__()):
    stdp_learners[i].step(on_grad=True)

optimizer_gd.step()
optimizer_stdp.step()

以 STDPLearner 为代表的所有学习器都是 MemoryModule 的子类，其内部记忆状态包括了突触前后神经元的迹 trace_pre, trace_post ；另外，学习器内部用于记录神经元活动的监视器存储了突触前后神经元的发放历史；这些发放历史也可以视作学习器的内部记忆状态。因此，必须及时调用学习器的 reset() 方法，来清空其内部记忆状态，从而防止内存/显存消耗量随着训练而不断增长！通常的做法是：在每个batch结束后，将学习器和网络一起重制：

functional.reset_net(net)
for i in range(stdp_learners.__len__()):
    stdp_learners[i].reset()

完整的示例代码如下：

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.optim import SGD, Adam
from spikingjelly.activation_based import learning, layer, neuron, functional

T = 8
N = 2
C = 3
H = 32
W = 32
lr = 0.1
tau_pre = 2.
tau_post = 100.
step_mode = 'm'

def f_weight(x):
    return torch.clamp(x, -1, 1.)


net = nn.Sequential(
    layer.Conv2d(3, 16, kernel_size=3, stride=1, padding=1, bias=False),
    neuron.IFNode(),
    layer.MaxPool2d(2, 2),
    layer.Conv2d(16, 16, kernel_size=3, stride=1, padding=1, bias=False),
    neuron.IFNode(),
    layer.MaxPool2d(2, 2),
    layer.Flatten(),
    layer.Linear(16 * 8 * 8, 64, bias=False),
    neuron.IFNode(),
    layer.Linear(64, 10, bias=False),
    neuron.IFNode(),
)

functional.set_step_mode(net, step_mode)

instances_stdp = (layer.Conv2d, )

stdp_learners = []

for i in range(net.__len__()):
    if isinstance(net[i], instances_stdp):
        stdp_learners.append(
            learning.STDPLearner(step_mode=step_mode, synapse=net[i], sn=net[i+1], tau_pre=tau_pre, tau_post=tau_post,
                                f_pre=f_weight, f_post=f_weight)
        )


params_stdp = []
for m in net.modules():
    if isinstance(m, instances_stdp):
        for p in m.parameters():
            params_stdp.append(p)

params_stdp_set = set(params_stdp)
params_gradient_descent = []
for p in net.parameters():
    if p not in params_stdp_set:
        params_gradient_descent.append(p)

optimizer_gd = Adam(params_gradient_descent, lr=lr)
optimizer_stdp = SGD(params_stdp, lr=lr, momentum=0.)



x_seq = (torch.rand([T, N, C, H, W]) > 0.5).float()
target = torch.randint(low=0, high=10, size=[N])

optimizer_gd.zero_grad()
optimizer_stdp.zero_grad()

y = net(x_seq).mean(0)
loss = F.cross_entropy(y, target)
loss.backward()



optimizer_stdp.zero_grad()

for i in range(stdp_learners.__len__()):
    stdp_learners[i].step(on_grad=True)

optimizer_gd.step()
optimizer_stdp.step()

functional.reset_net(net)
for i in range(stdp_learners.__len__()):
    stdp_learners[i].reset()

[1]

Bi, Guo-qiang, and Mu-ming Poo. “Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type.” Journal of neuroscience 18.24 (1998): 10464-10472.

[2]

Froemke, Robert C., et al. “Contribution of individual spikes in burst-induced long-term synaptic modification.” Journal of neurophysiology (2006).

[3] (1,2)

Morrison, Abigail, Markus Diesmann, and Wulfram Gerstner. “Phenomenological models of synaptic plasticity based on spike timing.” Biological cybernetics 98.6 (2008): 459-478.