Single Fully Connected Layer SNN to Classify MNIST

The tutorial will introduce how to train a simple SNN using the encoder and the surrogate gradient method to classify MNIST.

Build a simple SNN

When building neural networks with PyTorch, we can simply use nn.Sequential to stack layers to get a feedforward network, where input data will flow through each layer in order to get the output.

MNIST dataset contains 8-bit grey-scale images whose size is \(28\times 28\) and category is from 1 to 10. A simple single layer ANN to classify MNIST is as follows:

nn.Sequential(
    nn.Flatten(),
    nn.Linear(28 * 28, 10, bias=False),
    nn.Softmax()
    )

A SNN with similar structures can also be used for classification tasks. For this network, all activation functions should be replaced with spiking neurons (LIF neurons are used here), and the connetions between neurons should be packaged with spikingjelly.activation_based.layer :

nn.Sequential(
    layer.Flatten(),
    layer.Linear(28 * 28, 10, bias=False),
    neuron.LIFNode(tau=tau, surrogate_function=surrogate.ATan())
    )

The membrane potential constant \(\tau\) is set by tau , and surrogate.ATan is used as the surrogate gradient function.

Train the SNN

Training parameters like learning rate and other configurations need to be set:

Adam is used as the optimizer by default, and the poisson encoder is used to encode input images as spikes.

# Use Adam optimizer
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
# Use PoissonEncoder
encoder = encoding.PoissonEncoder()

There are three key points to follow when programing training codes:

The output of the spiking neuron is binary, and the output of a single run is easily disturbed by the noise caused by coding. Therefore, it is generally to consider the firing rate of the output layer in a period of time as the output of SNN. The value of the firing rate indicates the response intensity of the corresponding category. So we should run the SNN for a period of time T and take the average firing rate in T as classifying evidence.
The ideal outcome is that except for the proper neurons firing at the highest rate, the other neurons keep silent. Cross-entropy loss or MSE loss is often used. Here we use MSE loss for its better effect.
After each network simulation, the network state should be reset by functional.reset_net(net).

The core training codes are as follows:

for epoch in range(start_epoch, args.epochs):
    start_time = time.time()
    net.train()
    train_loss = 0
    train_acc = 0
    train_samples = 0
    for img, label in train_data_loader:
        optimizer.zero_grad()
        img = img.to(args.device)
        label = label.to(args.device)
        label_onehot = F.one_hot(label, 10).float()

        # Mixed-precision training
        if scaler is not None:
            with amp.autocast():
                out_fr = 0.
                # Run T time steps
                for t in range(args.T):
                    encoded_img = encoder(img)
                    out_fr += net(encoded_img)
                out_fr = out_fr / args.T
                # out_fr is tensor whose shape is [batch_size, 10]
                # The firing rate of 10 neurons in the output layer was recorded during the whole simulation period
                loss = F.mse_loss(out_fr, label_onehot)
                # The loss function is the MSE between the firing rate of the output layer and the true category.
                # The loss function will cause the firing rate of the correct neuron in the output layer to approach 1 when the label i is given, and the firing rate of the other neurons to approach 0.
            scaler.scale(loss).backward()
            scaler.step(optimizer)
            scaler.update()
        else:
            out_fr = 0.
            for t in range(args.T):
                encoded_img = encoder(img)
                out_fr += net(encoded_img)
            out_fr = out_fr / args.T
            loss = F.mse_loss(out_fr, label_onehot)
            loss.backward()
            optimizer.step()

        train_samples += label.numel()
        train_loss += loss.item() * label.numel()
        # The correct rate is calculated as follows. The subscript i of the neuron with the highest firing rate in the output layer is considered as the result of classification.
        train_acc += (out_fr.argmax(1) == label).float().sum().item()

        # After optimizing the parameters, the state of the network should be reset because the neurons of the SNN have “memory”.
        functional.reset_net(net)

The complete code is in activation_based.examples.lif_fc_mnist.py , where Tensorboard is used to save training logs. It can be run in the command line as follows:

$ python -m spikingjelly.activation_based.examples.lif_fc_mnist --help
usage: lif_fc_mnist.py [-h] [-T T] [-device DEVICE] [-b B] [-epochs N] [-j N]
                    [-data-dir DATA_DIR] [-out-dir OUT_DIR]
                    [-resume RESUME] [-amp] [-opt {sgd,adam}]
                    [-momentum MOMENTUM] [-lr LR] [-tau TAU]

LIF MNIST Training

optional arguments:
-h, --help          show this help message and exit
-T T                simulating time-steps
-device DEVICE      device
-b B                batch size
-epochs N           number of total epochs to run
-j N                number of data loading workers (default: 4)
-data-dir DATA_DIR  root dir of MNIST dataset
-out-dir OUT_DIR    root dir for saving logs and checkpoint
-resume RESUME      resume from the checkpoint path
-amp                automatic mixed precision training
-opt {sgd,adam}     use which optimizer. SGD or Adam
-momentum MOMENTUM  momentum for SGD
-lr LR              learning rate
-tau TAU            parameter tau of LIF neuron

It should be noted that the amount of memory required to train such an SNN is linearly related to the simulation time T. A larger T is equivalent to using a smaller simulation time step, and the training is more “refined” but not necessarily better. When T is too large, the SNN unfolds in time and becomes a very deep network, which will cause BPTT to decay or explode when calculating the gradient.

In addition, since we use the poisson encoder, a large T is needed to ensure that the coding noise is not too large.

Results of Training

We set tau=2.0,T=100,batch_size=64,lr=1e-3 , the corresponding command is:

python -m spikingjelly.activation_based.examples.lif_fc_mnist -tau 2.0 -T 100 -device cuda:0 -b 64 -epochs 100 -data-dir <PATH to MNIST> -amp -opt adam -lr 1e-3 -j 8

In order to speed up training, mixed precision training is used. After 100 Epoch training, two npy files and a training log are output. The highest accuracy on the test dataset is 92.9%. The accuracy curve visualized by matplotlib is as follows:

Select the first image in the test dataset:

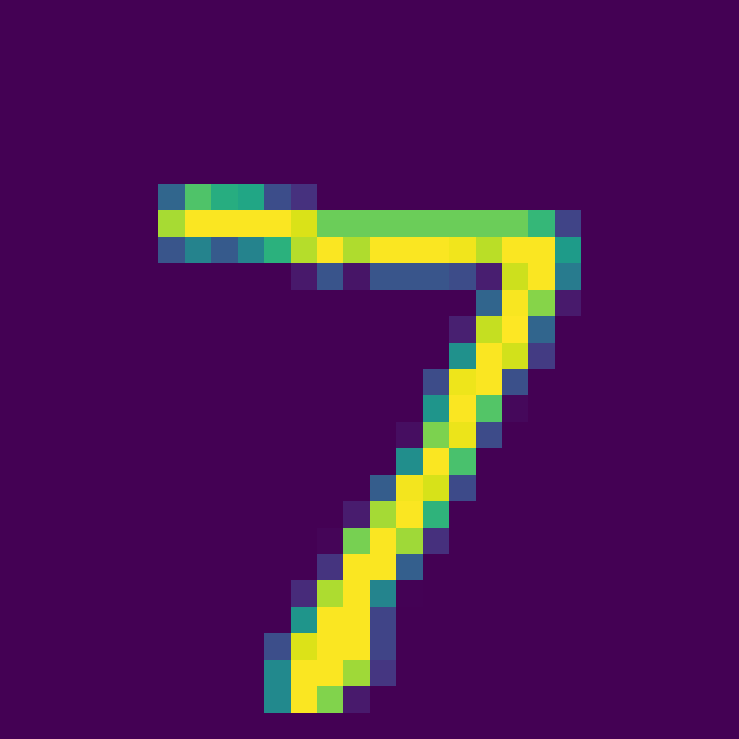
The classification results are obtained by using the trained model:

Firing rate: [[0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]]

Voltages and spikes are as follows, which are gotten by the visualization function in the visualizing module.

Obviously, except for the corresponding neuron in the correct category, no other neurons are firing. The complete training code is in activation_based/examples/lif_fc_mnist.py .