Neuron
Author: fangwei123456
This tutorial is about spikingjelly.activation_based.neuron and introduces the spiking neurons.
Spiking Neuron Modules
In SpikingJelly, we define the spiking neuron as the neuron that can only output spikes (or tensor whose element can only be 0 or 1). The network which uses spiking neurons is the Spiking Neural Network (SNN). Many frequently-used spiking neurons are defined in spikingjelly.activation_based.neuron. Let us use the spikingjelly.activation_based.neuron.IFNode as the example to learn how to use neurons in SpikingJelly.
Firstly, let us import modules:
import torch
from spikingjelly.activation_based import neuron
from spikingjelly import visualizing
from matplotlib import pyplot as plt
Define an IF neurons layer:
if_layer = neuron.IFNode()
There are some parameters for building IF neurons, and we can refer to API docs for more details. For the moment, we just focus on the following parameters:
v_threshold – threshold of this neurons layer
- v_reset – reset voltage of this neurons layer. If not
None, the neuron’s voltage will be set tov_resetafter firing a spike. If
None, the neuron’s voltage will subtractv_thresholdafter firing a spikesurrogate_function – the function for calculating surrogate gradients of the heaviside step function in backward
The user may be curious about how many neurons are in this layer. In most of the neurons layer in spikingjelly.activation_based.neuron.IFNode, the number of neurons is defined by the shape of input after this layer is initialized or reset().
Similar to RNN cells, the spiking neuron is stateful (or has memory). The state of spiking neurons is the membrane potentials \(V[t]\). All neurons in spikingjelly.activation_based.neuron have the attribute v. We can print the v:
print(if_layer.v)
# if_layer.v=0.0
We can find that if_layer.v is 0.0 because we have not given the neurons layer any input. Let us give different inputs and check the v.shape. We can find that it is the same with the input:
x = torch.rand(size=[2, 3])
if_layer(x)
print(f'x.shape={x.shape}, if_layer.v.shape={if_layer.v.shape}')
# x.shape=torch.Size([2, 3]), if_layer.v.shape=torch.Size([2, 3])
if_layer.reset()
x = torch.rand(size=[4, 5, 6])
if_layer(x)
print(f'x.shape={x.shape}, if_layer.v.shape={if_layer.v.shape}')
# x.shape=torch.Size([4, 5, 6]), if_layer.v.shape=torch.Size([4, 5, 6])
if_layer.reset()
Note that the spiking neurons are stateful. So, we must call reset() before we give a new input sample to the spiking neurons.
What is teh realization between \(V[t]\) and \(X[t]\)? In spiking neurons, \(V[t]\) is not determined by the input \(X[t]\) at the current time-step t, but also by the membrane potential \(V[t-1]\) at the last time-step t-1.
We use the sub-threshold neuronal dynamics \(\frac{\mathrm{d}V(t)}{\mathrm{d}t} = f(V(t), X(t))\) to describe the charging of continuous-time spiking neurons. For the IF neuron, the charging function is:
spikingjelly.activation_based.neuron uses the discrete-time difference equation to approximate the continuous-time ordinary differential equation. The discrete-time difference equation of the IF neuron is:
\(V[t]\) can be got by
We can find the following codes in spikingjelly.activation_based.neuron.IFNode.neuronal_charge:
def neuronal_charge(self, x: torch.Tensor):
self.v = self.v + x
Different spiking neurons have different charging equations. But after the membrane potential exceeds the threshold voltage, the firing and resetting equations are the same. Hence, these equations are inherited from spikingjelly.activation_based.neuron.BaseNode. We can find the codes in spikingjelly.activation_based.neuron.BaseNode.neuronal_fire:
def neuronal_fire(self):
self.spike = self.surrogate_function(self.v - self.v_threshold)
surrogate_function() is the Heaviside step function in forward, which returns 1 when input is greater or equal to 0, otherwise returns 0. We regard the tensor whose element is only 0 or 1 as the spike.
Firing spike will consume the accumulated potential, and make the potential decrease instantly, which is the neuronal reset. In SNN, there are two kinds of reset:
Hard reset: the membrane potential will be set to the reset voltage after firing: \(V[t] = V_{reset}\)
Soft reset: the membrane potential will decrease the threshold potential after firing: \(V[t] = V[t] - V_{threshold}\)
We can find that the neuron that uses soft reset does not need the attribute \(V_{reset}\). The default value of v_reset in the __init__ function of spikingjelly.activation_based.neuron is 1.0 and the neuron will use hard reset by default.If we set v_reset = None, then the neuron will use the soft reset. We can find the codes for neuronal reset in spikingjelly.activation_based.neuron.BaseNode.neuronal_fire.neuronal_reset:
# The following codes are for tutorials. The actual codes are different but have similar behavior.
def neuronal_reset(self):
if self.v_reset is None:
self.v = self.v - self.spike * self.v_threshold
else:
self.v = (1. - self.spike) * self.v + self.spike * self.v_reset
Three equations for describing spiking neurons
Now we can use the three equations: neuronal charge, neuronal fire, and neuronal reset, to describe all kinds of spiking neurons:
where \(\Theta(x)\) is the surrogate_function in the parameters of __init__. \(\Theta(x)\) is the heaviside step function:
The hard reset equation is:
The soft reset equation is:
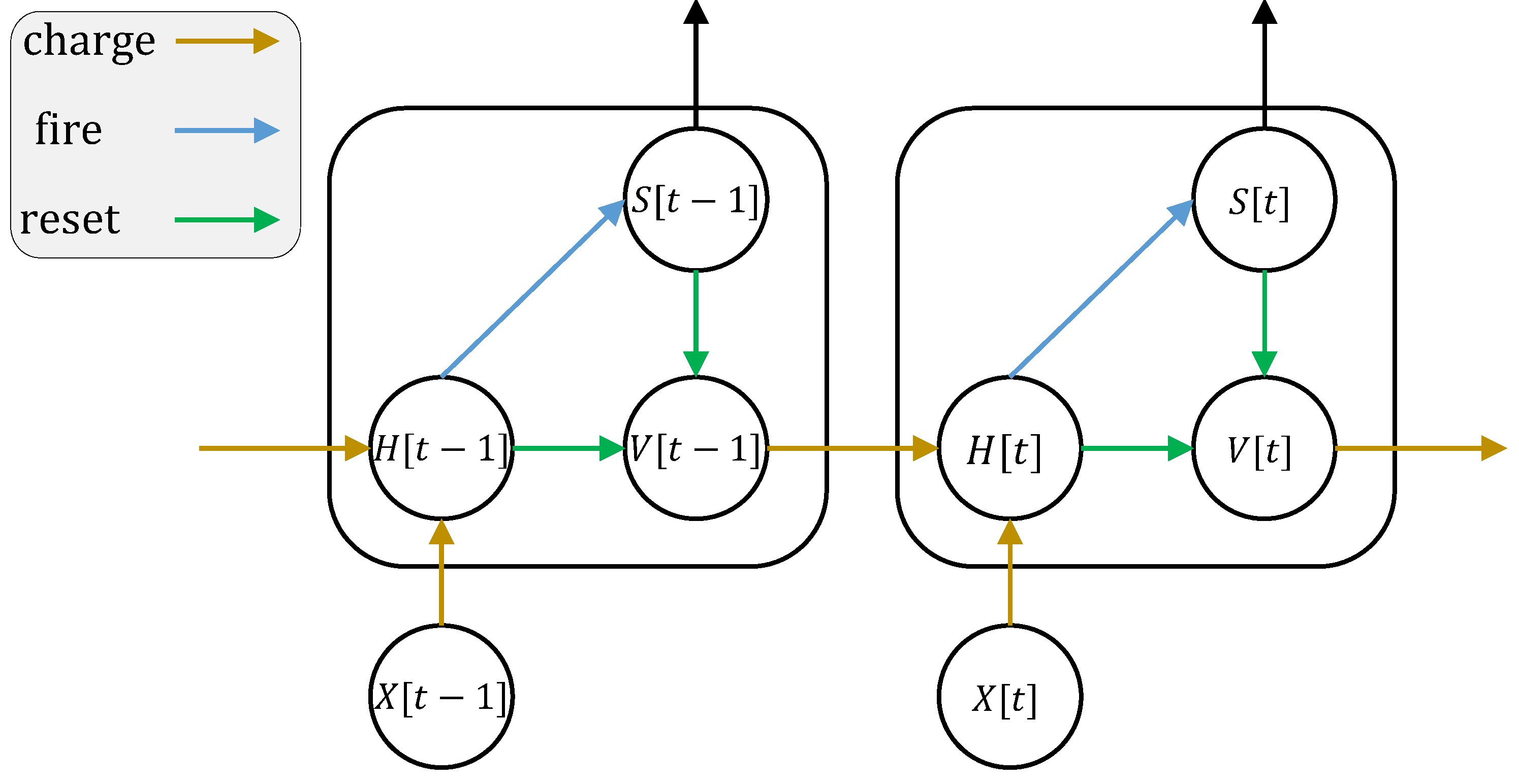
where \(X[t]\) is the external input. To avoid confusion, we use \(H[t]\) to represent the membrane potential after neuronal charging but before neuronal firing. \(V[t]\) is the membrane potential after neuronal firing. \(f(V[t-1], X[t])\) is the neuronal charging function, and is different for different neurons.
The neuronal dynamics can be described by the following figure (the figure is cited from Incorporating Learnable Membrane Time Constant to Enhance Learning of Spiking Neural Networks):
Simulation
Now let us give inputs to the spiking neurons step-by-step, check the membrane potential and output spikes, and plot them:
if_layer.reset()
x = torch.as_tensor([0.02])
T = 150
s_list = []
v_list = []
for t in range(T):
s_list.append(if_layer(x))
v_list.append(if_layer.v)
dpi = 300
figsize = (12, 8)
visualizing.plot_one_neuron_v_s(torch.cat(v_list).numpy(), torch.cat(s_list).numpy(), v_threshold=if_layer.v_threshold,
v_reset=if_layer.v_reset,
figsize=figsize, dpi=dpi)
plt.show()
The input has shape=[1]. So, there is only 1 neuron. Its membrane potential and output spikes are:
Reset the neurons layer, and give the input with shape=[32]. Then we can check the membrane potential and output spikes of these 32 neurons:
if_layer.reset()
T = 50
x = torch.rand([32]) / 8.
s_list = []
v_list = []
for t in range(T):
s_list.append(if_layer(x).unsqueeze(0))
v_list.append(if_layer.v.unsqueeze(0))
s_list = torch.cat(s_list)
v_list = torch.cat(v_list)
figsize = (12, 8)
dpi = 200
visualizing.plot_2d_heatmap(array=v_list.numpy(), title='membrane potentials', xlabel='simulating step',
ylabel='neuron index', int_x_ticks=True, x_max=T, figsize=figsize, dpi=dpi)
visualizing.plot_1d_spikes(spikes=s_list.numpy(), title='membrane sotentials', xlabel='simulating step',
ylabel='neuron index', figsize=figsize, dpi=dpi)
plt.show()
The results are:
Step mode and backend
We have introduced step modes in Basic Conception. In the above codes, we use the single-step mode. By setting step_mode, we can switch to multi-step easily:
import torch
from spikingjelly.activation_based import neuron, functional
if_layer = neuron.IFNode(step_mode='s')
T = 8
N = 2
x_seq = torch.rand([T, N])
y_seq = functional.multi_step_forward(x_seq, if_layer)
if_layer.reset()
if_layer.step_mode = 'm'
y_seq = if_layer(x_seq)
if_layer.reset()
In addition, some neurons support for cupy backend when using multi-step mode. cupy backend can accelerate forward and backward:
import torch
from spikingjelly.activation_based import neuron
if_layer = neuron.IFNode()
print(f'if_layer.backend={if_layer.backend}')
# if_layer.backend=torch
print(f'step_mode={if_layer.step_mode}, supported_backends={if_layer.supported_backends}')
# step_mode=s, supported_backends=('torch',)
if_layer.step_mode = 'm'
print(f'step_mode={if_layer.step_mode}, supported_backends={if_layer.supported_backends}')
# step_mode=m, supported_backends=('torch', 'cupy')
device = 'cuda:0'
if_layer.to(device)
if_layer.backend = 'cupy' # switch to the cupy backend
print(f'if_layer.backend={if_layer.backend}')
# if_layer.backend=cupy
x_seq = torch.rand([8, 4], device=device)
y_seq = if_layer(x_seq)
if_layer.reset()
Custom Spiking Neurons
As mentioned above, SpikingJelly uses three equations: neuronal change, neuronal fire, and neuronal reset, to describe all kinds of spiking neurons.We can find the corresponding codes in BaseNode. The forward of single-step, which is the single_step_forward function, is composed of the three equations:
# spikingjelly.activation_based.neuron.BaseNode
def single_step_forward(self, x: torch.Tensor):
self.neuronal_charge(x)
spike = self.neuronal_fire()
self.neuronal_reset(spike)
return spike
neuronal_fire and neuronal_reset are same for most spiking neurons, and are defined by BaseNode. The difference of neurons are __init__ and neuronal_charge functions.Hence, if we want to implement a new kind of spiking neuron, we only need to change the __init__ and neuronal_charge functions.
Suppose we want to build a Square-Integrated-and-Fire neuron, whose neuronal charge equation is:
We can implement this kind of neuron by the following codes:
import torch
from spikingjelly.activation_based import neuron
class SquareIFNode(neuron.BaseNode):
def neuronal_charge(self, x: torch.Tensor):
self.v = self.v + x ** 2
BaseNode is inherited from MemoryModule, which uses for t in range(T) to call single-step forward function to implement the multi-step forward by default. So, after we define the neuronal_charge, then single_step_forward is completed, and multi_step_forward is also completed.
Use our SquareIFNode to implement the single/multi-step forward:
import torch
from spikingjelly.activation_based import neuron
class SquareIFNode(neuron.BaseNode):
def neuronal_charge(self, x: torch.Tensor):
self.v = self.v + x ** 2
sif_layer = SquareIFNode()
T = 4
N = 1
x_seq = torch.rand([T, N])
print(f'x_seq={x_seq}')
for t in range(T):
yt = sif_layer(x_seq[t])
print(f'sif_layer.v[{t}]={sif_layer.v}')
sif_layer.reset()
sif_layer.step_mode = 'm'
y_seq = sif_layer(x_seq)
print(f'y_seq={y_seq}')
sif_layer.reset()
The outputs are:
x_seq=tensor([[0.7452],
[0.8062],
[0.6730],
[0.0942]])
sif_layer.v[0]=tensor([0.5554])
sif_layer.v[1]=tensor([0.])
sif_layer.v[2]=tensor([0.4529])
sif_layer.v[3]=tensor([0.4618])
y_seq=tensor([[0.],
[1.],
[0.],
[0.]])