Clock driven: Use single-layer fully connected SNN to identify MNIST
Author: Yanqi-Chen
Translator: YeYumin
This tutorial will introduce how to train a simplest MNIST classification network using encoders and alternative gradient methods.
Build a simple SNN network from scratch
When building a neural network in PyTorch, we can simply usenn.Sequentialto stack multiple network layers to get a
feedforward network. The input data will flow through each network layer in order to get the output.
The MNIST Dateset contains several 8-bit grayscale images with the size of \(28\times 28\), which include total of 10 categories from 0 to 9. Taking the classification of MNIST as an example, a simple single-layer ANN network is as follows:
net = nn.Sequential(
nn.Flatten(),
nn.Linear(28 * 28, 10, bias=False),
nn.Softmax()
)
We can also use SNN with a completely similar structure for classification tasks. As far as this network is concerned, we only need to remove all the activation functions first, and then add the neurons to the original activation function position. Here we choose the LIF neuron:
net = nn.Sequential(
nn.Flatten(),
nn.Linear(28 * 28, 10, bias=False),
neuron.LIFNode(tau=tau)
)
Among them, the membrane potential decay constant \(\tau\) needs to be set by the parameter tau.
Train SNN network
First specify the training parameters such as learning rate and several other configurations
The optimizer uses Adam and Poisson encoder to perform spike encoding every time when a picture is input.
# Use Adam optimizer
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
# Use Poisson encoder
encoder = encoding.PoissonEncoder()
The writing of training code needs to follow the following three points:
The output of the spiking neuron is binary, and directly using the result of a single run for classification is very susceptible to interference. Therefore, it is generally considered that the output of the spike network is the firing frequency (or firing rate) of the output layer over a period of time, and the firing rate indicates the response strength of the category. Therefore, the network needs to run for a period of time, that is, the average distribution rate after
Ttime is used as the classification basis.The desired result we hope is that except for the correct neuron firing the highest frequency, the other neurons remain silent. Cross-entropy loss or MSE loss is often used, and here we use MSE loss which have a better actual effect.
After each network simulation is over, the network status needs to be reset.
Combining the above three points, the code of training loop is as follows:
print("Epoch {}:".format(epoch))
print("Training...")
train_correct_sum = 0
train_sum = 0
net.train()
for img, label in tqdm(train_data_loader):
img = img.to(device)
label = label.to(device)
label_one_hot = F.one_hot(label, 10).float()
optimizer.zero_grad()
# Run for T durations, out_spikes_counter is a tensor with shape=[batch_size, 10]
# Record the number of spikes delivered by the 10 neurons in the output layer during the entire simulation duration
for t in range(T):
if t == 0:
out_spikes_counter = net(encoder(img).float())
else:
out_spikes_counter += net(encoder(img).float())
# out_spikes_counter / T # Obtain the firing frequency of 10 neurons in the output layer within the simulation duration
out_spikes_counter_frequency = out_spikes_counter / T
# The loss function is the firing frequency of the neurons in the output layer, and the MSE of the real class
# Such a loss function causes that when the category i is input, the firing frequency of the i-th neuron in the output layer approaches 1, while the firing frequency of other neurons approaches 0.
loss = F.mse_loss(out_spikes_counter_frequency, label_one_hot)
loss.backward()
optimizer.step()
# After optimizing the parameters once, the state of the network needs to be reset, because the SNN neurons have "memory"
functional.reset_net(net)
# Calculation of accuracy. The index of the neuron with max frequency in the output layer is the classification result.
train_correct_sum += (out_spikes_counter_frequency.max(1)[1] == label.to(device)).float().sum().item()
train_sum += label.numel()
train_batch_accuracy = (out_spikes_counter_frequency.max(1)[1] == label.to(device)).float().mean().item()
writer.add_scalar('train_batch_accuracy', train_batch_accuracy, train_times)
train_accs.append(train_batch_accuracy)
train_times += 1
train_accuracy = train_correct_sum / train_sum
The complete code is located in clock_driven.examples.lif_fc_mnist.py. In the code, we also use Tensorboard to
save training logs. You can run it directly on the command line:
$ python <PATH>/lif_fc_mnist.py --help
usage: lif_fc_mnist.py [-h] [--device DEVICE] [--dataset-dir DATASET_DIR] [--log-dir LOG_DIR] [-b BATCH_SIZE] [-T T] [--lr LR] [--gpu GPU]
[--tau TAU] [-N EPOCH]
spikingjelly MNIST Training
optional arguments:
-h, --help show this help message and exit
--device DEVICE 运行的设备,例如“cpu”或“cuda:0” Device, e.g., "cpu" or "cuda:0"
--dataset-dir DATASET_DIR
保存MNIST数据集的位置,例如“./” Root directory for saving MNIST dataset, e.g., "./"
--log-dir LOG_DIR 保存tensorboard日志文件的位置,例如“./” Root directory for saving tensorboard logs, e.g., "./"
-b BATCH_SIZE, --batch-size BATCH_SIZE
-T T, --timesteps T 仿真时长,例如“100” Simulating timesteps, e.g., "100"
--lr LR, --learning-rate LR
学习率,例如“1e-3” Learning rate, e.g., "1e-3":
--gpu GPU GPU id to use.
--tau TAU LIF神经元的时间常数tau,例如“100.0” Membrane time constant, tau, for LIF neurons, e.g., "100.0"
-N EPOCH, --epoch EPOCH
It should be noted that for training such an SNN, the amount of video memory required is linearly related to the
simulation duration T. A longer T is equivalent to using a smaller simulation step, and the training is more “fine”,
but the training effect is not necessarily better. When T is too large, the SNN will become a very deep network after
unfolding in time, which will cause the gradient to be easily attenuated or exploded.
In addition, because we use a Poisson encoder, a larger T is required.
Training result
Take tau=2.0,T=100,batch_size=128,lr=1e-3, after training 100 Epoch, four npy files will be output. The highest
correct rate on the test set is 92.5%, and the correct rate curve obtained through matplotlib visualization is as follows
Select the first picture in the test set:
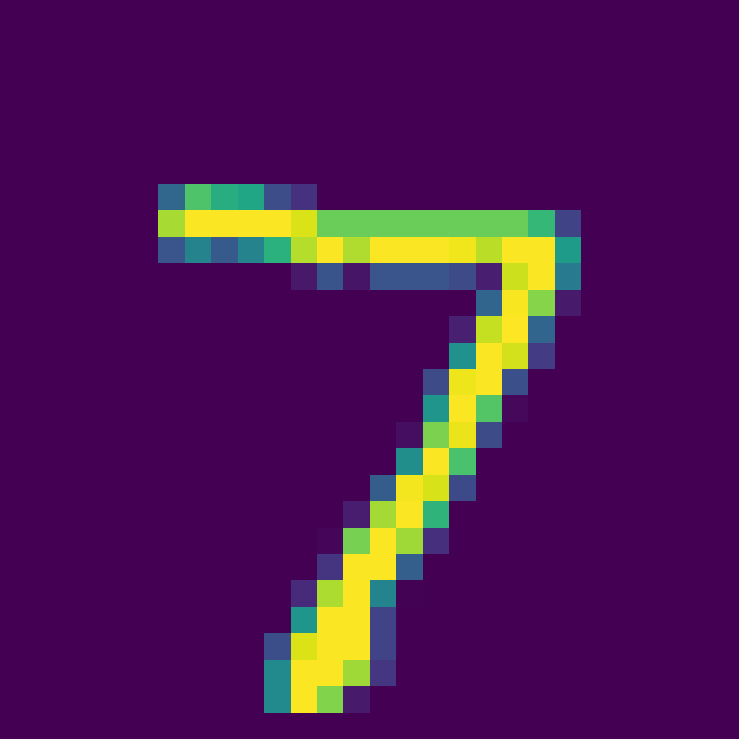
Use the trained model to classify and get the classification result.
Firing rate: [[0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]]
The voltage and spike of the output layer can be visualized by the function in the visualizing module as shown in the figure below.
It can be seen that none of the neurons emit any spikes except for the neurons corresponding to the correct category. The complete training code can be found in clock_driven/examples/lif_fc_mnist.py.